인공지능 중소벤처 제조 플랫폼 포털에서 데이터셋, 가이드북, 실습용 주피터노트북을 모두 다운받을 수 있습니다.
인공지능 중소벤처 제조 플랫폼
3축(x,y,z) 진동데이터 기반 설비 예지보전을 위한 교반구동장치 데이터 공유 --> 제조AI데이터셋 가이드북
kamp-ai.kr
0. 분석 프로세스

가이드북에는 총 9단계에 걸쳐서 데이터 분석을 진행하고 있습니다.
각 단계를 간략하게 요약하면서 제가 배운 부분 위주로 정리해 볼게요!
가이드북..매번 강조해도 아깝지 않습니다!!! 최고!
1단계. 라이브러리/데이터 불러오기
필요한 라이브러리를 불러옵니다
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn import neighbors
from math import sqrt
from sklearn.metrics import mean_squared_error
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.metrics import confusion_matrix, classification_report
import seaborn as sns
sns.set(font_scale=2)
import matplotlib.pyplot as plt
%matplotlib qt데이터를 불러옵니다
data = pd.read_csv('mixing_actuator.csv')
2단계. 데이터 기술통계
%matplotlib qt라는 매직 커맨드는 그래프를 출력할 때 새로운 창을 열고 그 안에 그래프를 표현하기 위해 사용합니다.
jupyter notebook 내에서 확인하면 화면 크기 조정에 제한이 있어서 화면 조정을 자유롭게 하기 위해 활용한다고 하네요!
plt.plot(data['Sensor'])
plt.show()
코드에서는 x축과 y축을 설정하지 않았지만, 데이터는 순차적으로 출력되었기 때문에
x축은 '시간의 흐름'으로 간주하고, y축은 '센서데이터(진동)'을 의미합니다.
진동데이터가 어떤 패턴을 띄는지 확인할 수 있습니다
data['Sensor'].describe() # describe()로 연속형 변수의 기술통계 확인
data['Quality'].value_counts() #valud_counts()로 범주형 변수의 기술통계 확인
3단계. 데이터 집단 구분
데이터 파일을 한번 불러오면 인덱스 변수가 생성되는데, 분석에 불필요하므로 먼저 제거합니다.
data = data.drop(['Unnamed: 0'], axis=1) #axis=1은 열 기준 해당 변수를 삭제한다.
센서데이터 변수에 초 단위의 시간을 반복적으로 매칭시켜 K-최근접 이웃 회귀를 위한 독립변수(시간)을 생성한다고 합니다. 이를 위해 1,024초를 불량 여부를 체크하는 하나의 시간 집단이라고 가정하고,
1~1,024초가 데이터의 수대로 반복되도록 시간집단을 생성합니다.
(이 부분이 KNN 회귀에서 중요한 부분인 것 같은데,,,, 이게 무슨 소리인지 아직 이해를 충분히 다 못 했어요. 이 부분은 심화공부를 더 해보는 것으로...!!!)
sec = [] #시간 리스트를 보관할 빈 리스트를 생성한다.
sec_num = 0
#for문(반복문)내에서 초기 설정하지 않아도 되도록 먼저 sec_num 변수를 지정한다.
for i in range(len(data)):
sec_num += 1
sec.append(sec_num)
if sec_num == 1024: #1024초 간격으로 집단을 형성한다.
sec_num = 0 #1024인 sec_num을 리스트에 넣고 나서 다시 0으로 리셋시킨다.
else:
sec_num = sec_num
sec[1000:1050]
분석과정에서 data의 Sensor변수가 종속변수이고, sec의 시간을 독립변수로 설정하기 때문에
위의 코드에서 생성한 sec를 data에 추가해줍니다.
data['sec'] = sec
data[0:1025] #데이터를 슬라이스해서 확인한다.
4단계. 훈련용, 시험용 데이터 구분
독립변수와 종속변수를 설정해줍니다.
X = data['sec'] # 독립변수 : 매칭시킨 패턴 내 시간
y = data['Sensor'] # 종속변수 : 센서 데이터 1개의 변수
훈련용/시혐용 데이터를 구분해줍니다.
# 데이터셋을 훈련 세트와 테스트 세트로 나눈다.
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2, random_state=0, shuffle=False)
X_train = X_train.values
X_test = X_test.values
y_train = y_train.values
y_test = y_test.valuesreshape을 통해 알고리즘을 구현할 때 X_train과 X_test를 적용할 수 있도록 형태를 변형합니다.
y_train과 y_test에는 reshape 과정이 필요하지 않으므로 건너뜁니다.
X_train.shape, X_test.shape #((280985,), (70247,))
# reshape 적용
X_train = X_train.reshape(X_train.shape[0], 1)
X_test = X_test.reshape(X_test.shape[0], 1)
# reshape 적용 후 데이터 shape 확인
X_train.shape, X_test.shape #((280985, 1), (70247, 1))
5단계. 하이퍼파라미터 탐색
RMSE를 이용해서 최적의 k값을 탐색합니다.
rmse_val = []
for K in range(30):
K = K+1
model = neighbors.KNeighborsRegressor(n_neighbors = K,
weights = 'distance')
model.fit(X_train, y_train) #데이터를 모델에 적용한다.
pred=model.predict(X_test) #모델의 학습 내용을 가지고 X_test로 예측한다.
error = sqrt(mean_squared_error(y_test,pred)) #RMSE를 계산한다.
rmse_val.append(error) #RMSE를 계속해서 보관해둔다.
print('RMSE value for k= ', K , 'is:', error)가이드북에서는 range를 17로 설정했는데, 저는 언제까지 RMSE 값이 낮아지는지 궁금해서 계속 높이다가 30에서 멈췄습니다.
range가 30이어도 계속 RMSE값이 낮아지길래, 저는 k=30으로 KNN 회귀를 진행했습니다.
그래서 이제부터 나오는 결과는 가이드북과 조금 다를 수 있어요!

K값별 RMSE 계산 결과를 그래프로 그려봅니다
curve = pd.DataFrame(rmse_val)
curve.plot()
K가 증가할수록 RMSE가 감소하면서 일정하게 낮은 값을 유지하는 것을 확인할 수 있습니다.
6단계. 모델 학습
KNN 회귀 결과에서 모델의 설명력을 시그모이드 함수를 이용해 계산하기 위해 sigmoid() 함수를 자체적으로 설정합니다.
def sigmoid(x):
return 1 / (1 +np.exp(-x)) 데이터셋에 특성값을 만들어 예측할 수 있습니다.
X축을 따라 많은 포인트를 생성해서 예측이 잘 이루어졌는지 확인하고 표준데이터를 추출하기 위해 별도의 데이터셋(line)을 만듭니다.
1부터 a사이에 b개의 데이터 포인트를 만들기 위해 np.linspace(start, stop, num)을 수행하고
reshape을 이용해 predict에 적합한 형태로 변환합니다.
line = np.linspace(1, 1024, 1024).reshape(-1, 1)reshape(-1, 1) 의 뜻을 몰랐는데, rfriend님이 자세하게 설명해주셨어요!
[Python NumPy] reshape에서 -1 은 무슨 의미인가? (reshape(-1, 1))
파이썬 NumPy 에서 배열의 차원(Dimension)을 재구조화, 변경하고자 할 때 reshape() 메소드를 사용합니다. 가령, 3개의 행과 4개의 열로 구성된 2차원의 배열로 재설정하고 싶으면 reshape(3, 4) 처럼 reshape(
rfriend.tistory.com
reshape()의 '-1'은 변경된 배열의 '-1'위치의 차원은 "원래 배열의 길이와 남은 차원으로부터 추정"이 된다는 뜻이라
가이드북에서의 reshape(-1, 1)은 1024행 1열의 배열이 됩니다.
최적의 K로 추출된 30을 n_neighbors에 할당해서 KNN 회귀의 k를 30으로 지정하고 모델을 적합시킵니다.
#적합한 K를 적용하여 reg.predict(line)을 수행한다.
reg = KNeighborsRegressor(n_neighbors=30, weights = 'distance')
reg.fit(X_train, y_train)
standard = reg.predict(line)
print(standard)
print(len(standard)) #표준 데이터의 길이를 확인한다.
모델 적합 이후에 상한/하한 임계치를 추출하는 작업을 진행합니다.
#표준 데이터의 표준편차를 추출한다.
sigma = np.std(standard)
print(sigma) #표준편차를 확인한다.상한/하한 임계치는 '표준데이터 ± 3*표준편차'로 설정합니다.
min_standard = standard - 3*sigma #하한 임계치
max_standard = standard + 3*sigma #상한 임계치상한/하한/표준 임계치를 y_test길이만큼 반복해서 리스트로 생성합니다. (dataframe에 붙이기 전 작업)
#y_test 길이만큼 최소 임계치 반복
min_standard_list = []
j = 0
for i in range(len(y_test)):
min_standard_list.append(min_standard[j])
j += 1
if j == len(min_standard):
j = 0 #초기화한다.
#y_test 길이만큼 최대 임계치를 반복시킨다.
max_standard_list = []
j = 0
for i in range(len(y_test)):
max_standard_list.append(max_standard[j])
j += 1
if j == len(max_standard):
j = 0 #초기화한다.
#y_test 길이만큼 표준 임계치 반복시킨다.
standard_list = []
j = 0
for i in range(len(y_test)):
standard_list.append(standard[j])
j += 1
if j == len(standard):
j = 0 #초기화한다.실제 y값, 표준데이터, 하한 임계치, 상한 임계치를 하나의 데이터프레임에 모아 df라는 객체에 저장합니다.
df = pd.DataFrame({'real_y':y_test, 'standard':standard_list,
'min_standard':min_standard_list,
'max_standard':max_standard_list})
7단계. 모델 평가
df 객체 안에 있는 데이터프레임에 pred_fault 변수를 추가하기 위해 pred_fault 리스트를 생성합니다.
이 리스트에는 실제 y값인 df 객체의 real_y 변수 내의 각각의 값들이 max_standard 변수(상한 임계치) 내의 값보다 크거나 min_standard 변수(하한 임계치) 내의 값보다 작을 경우 1의 값이 입력됩니다.
#하한, 상한 임계치를 y_test와 비교하여 예측 품질 컬럼을 추가한다.
pred_fault = []
for i in range(len(df)):
if df['real_y'][i] >= df['max_standard'][i] or df['real_y'][i] <= df['min_standard'][i]:
pred_fault.append(1)
else:
pred_fault.append(0)실제 Quality(불량인지 정상인지 나타내는 변수)를 리스트로 생성합니다
real_fault = []
for i in range(len(df)):
if data['Quality'][280985+i] == 'FAILED':
real_fault.append(1)
else:
real_fault.append(0)df 데이터프레임에 합체!
df['pred_fault'] = pred_fault
df['real_fault'] = real_fault
8단계. 모델 평가 결과 시각화
실제 센서 데이터 값과 표준데이터 값의 비교 그래프를 그려봅니다.
plt.figure(figsize=(15,4))
plt.plot(df['real_y'],'black', label='real_y')
plt.plot(df['min_standard'],'b', label='min')
plt.plot(df['max_standard'],'b', label='max')
plt.plot(df['standard'], 'r', label='standard')
plt.xlabel('Time')
plt.ylabel('Sensor Data')
plt.title('Fault Checking')
plt.legend(loc='best', ncol=4, fontsize=15)
plt.show()
시각적으로 어떤 시점의 값이 범위를 벗어나고 있는지 확인했다면
분류 성능 평가 척도를 산출합니다.
print('정밀도는',round(precision_score(df['real_fault'], df['pred_fault']), 2)*100, '% 입니다')
print('정확도는',round(accuracy_score(df['real_fault'], df['pred_fault']), 2)*100, '% 입니다')
print('재현율은',round(recall_score(df['real_fault'], df['pred_fault']), 2)*100, '% 입니다')
print('f1-score는',round(f1_score(df['real_fault'], df['pred_fault']), 2)*100, '% 입니다')
k=17로 설정한 가이드북의 결과와 비교했을 때,
정밀도, 정확률, f1-score는 낮게 나왔습니다. 재현율은 높게 나왔네요. 분석 목표 및 환경에 따라 k값을 설정해주면 될 것 같습니다.
혼동행렬(Confusion Matrix)와 분류 결과를 산출해봅니다.
print(confusion_matrix(df['real_fault'], df['pred_fault'], labels=[1,0]))
print(classification_report(df['real_fault'], df['pred_fault'], target_names=['정상', '불량']))
혼동행렬을 출력합니다
arr = [[28796, 173],
[13706, 27572]]
df_cm = pd.DataFrame(arr, index=[i for i in 'TF'], columns = ['T','F'])
plt.figure(figsize=(7,5)) #inch
plt.title('confusion matrix without normalization')
sns.heatmap(df_cm, annot=True, fmt='d', annot_kws={'size':30})
9단계. 결과 분석 및 해석
실제 불량횟수와 표준데이터를 이용한 불량 검출 횟수를 확인하면
예측품질(pred_fault)과 실제품질(real_fault)을 비교해 실제 불량 중 표준데이터를 이용한 불량 검출이 얼마나 잘 되었느지에 대한 재현율을 추출할 수 있습니다.
predict = 0
real= 0
for i in range(len(df)):
if df['real_fault'][i] == 1:
real += 1
else:
real = real
for j in range(len(df)):
if df['pred_fault'][j] == 1 and df['real_fault'][j] == 1:
predict += 1
else:
predict = predict
print('실제 불량 횟수:',real)
print('표준데이터를 이용한 불량 검출 횟수:', predict)
print('실제 불량 중 표준데이터를 이용하여 불량을 정확히 검출한 비율:', round(recall_score(df['real_fault'], df['pred_fault']), 2)*100,'%')
이번에는 임계치를 실제 y값의 평균을 구한 하나의 값이라고 가정한 뒤 불량을 예측하고 재현율을 검출해보겠습니다.
위와 비교한다면 표준데이터, 상한/하안 임계치의 효용성을 확인해볼 수 있고
비교결과에 따라 하나의 값으로만 설정한 임계치와 표준데이터를 이용한 임계치 중 어느 것의 결과가 더 좋은지 알 수 있습니다.
비교 (1) 평균보다 실제값이 클 때 불량이라고 설정
mean_data = df['real_y'].mean()
print(mean_data) # -0.14667287837914814
mean_pred = []
for a in range(len(df)):
if df['real_y'][a] > mean_data:
mean_pred.append(1)
else:
mean_pred.append(0)
df['mean_fault'] = mean_pred
predict = 0
real= 0
for i in range(len(df)):
if df['real_fault'][i] == 1:
real += 1
else:
real = real
for j in range(len(df)):
if df['mean_fault'][j] == 1 and df['real_fault'][j] == 1:
predict += 1
else:
predict = predict
print('실제 불량 횟수:',real)
print('평균 임계치보다 클 경우 불량을 검출한 횟수:', predict)
print('실제 불량 중 평균 임계치를 이용하여 불량을 정확히 검출한 비율:', round(recall_score(df['real_fault'], df['mean_fault'])*100, 2),'%')
비교 (2) 평균보다 실제값이 작을 때 불량이라고 설정
mean_pred = []
for a in range(len(df)):
if df['real_y'][a] < mean_data:
mean_pred.append(1)
else:
mean_pred.append(0)
df['mean_fault'] = mean_pred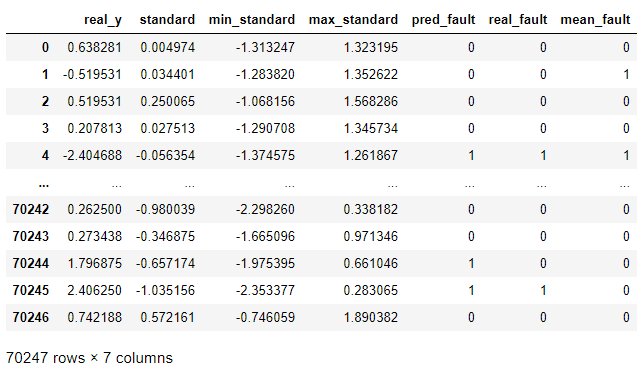
predict = 0
real= 0
for i in range(len(df)):
if df['real_fault'][i] == 1:
real += 1
else:
real = real
for j in range(len(df)):
if df['mean_fault'][j] == 1 and df['real_fault'][j] == 1:
predict += 1
else:
predict = predict
print('실제 불량 횟수:',real)
print('평균 임계치보다 작을 경우 불량을 검출한 횟수:', predict)
print('실제 불량 중 평균 임계치를 이용하여 불량을 정확히 검출한 비율:', round(recall_score(df['real_fault'], df['mean_fault'])*100, 2),'%')
표준데이터, 상한/하한 임계치를 사용한 재현율이 월등하게 높은 것을 확인할 수 있습니다.
<omg's comment>
KNN 회귀 알고리즘의 프로세스를 정확하게 알 수 있는 예제였습니다.
그리고 공부해서 채워넣어야 하는 부분이 있다면
(1) predict을 위해 reshape을 하는 이유
(2) 시간집단을 생성할 때 참고해야하는 근거가 있는지....?? (가이드북에서는 1024초로 가정했습니다.)
(3) sigmoid 함수로 모델의 설명력을 계산한다고 했는데.... 어디에서 사용한 것인지?? (저는 못 찾겠더라구요ㅠㅠ)
다음에도 좋은 포스팅으로 찾아뵙겠습니다
출처: 중소벤처기업부, Korea AI Manufacturing Platform(KAMP), 교반구동장치 AI데이터셋, KAIST(임픽스, 한양대학교 산학협력단, 아큐라소프트), 2020.12.14
'데이터 분석' 카테고리의 다른 글
| [의사결정나무] 개념 (0) | 2021.02.22 |
|---|---|
| [로지스틱 회귀분석] 개념 (0) | 2021.02.22 |
| [K-최근접이웃/KNN] 교반구동장치 AI 데이터셋 (1) (0) | 2021.01.09 |
| [의사결정나무/Decision Tree] 살균기 AI 데이터셋 (2) 실습/코드 (0) | 2021.01.05 |
| [의사결정나무/Decision Tree] 살균기 AI 데이터셋 (1) (0) | 2021.01.05 |

